1991. Максимальный поток
Найдите величину максимального потока в заданной сети.
Вход. В первой строке заданы два числа n и m (1
≤ n ≤ 100, 1 ≤ m ≤ 10000) –
соответственно количество вершин и рёбер в сети. Каждая из следующих m
строк содержит по три числа ui, vi и ci
(1 ≤ ui, vi ≤ n, 1
≤ ci ≤ 10000), означающих, что между вершинами ui
и vi в сети присутствует ребро с пропускной способностью ci.
Вершина 1 считается истоком, а вершина n стоком. Граф сети является
неориентированным и может содержать мультиребра. Все входные числа целые.
Выход. Выведите
величину максимального потока в заданной сети.
|
Пример
входа |
Пример
выхода |
3 31 2 31 3 5
3 2 7 |
8 |
РЕШЕНИЕ
графы –
максимальный поток
Анализ алгоритма
В задаче
достаточно реализовать алгоритм поиска максимального потока на неориентированном
графе с мультиребрами. Например, для нахождения дополняющего пути из истока в
сток воспользуемся поиском в глубину.
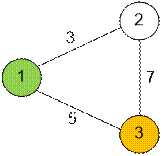
Пример
Граф, заданный в
тесте, имеет следующий вид. Исток отображен зеленым, а сток – оранжевым цветом.
Реализация алгоритма
Веса ребер графа
храним в матрице m. В массиве used будем отмечать посещенные вершины при
поиске в глубину.
#define MAX 120
int m[MAX][MAX], used[MAX];
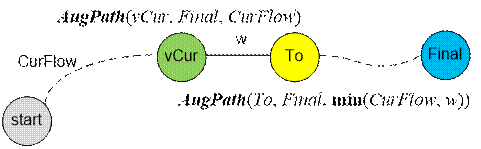
Функция AugPath(vCur,
Final, CurFlow) находит пропускную способность дополняющего пути
от вершины vCur до Final, если известно, что пропускная
способность дополняющего пути от начальной вершины до vCur равна CurFlow.
int AugPath(int
vCur, int Final, int
CurFlow)
{
if (vCur ==
Final) return CurFlow;
if
(used[vCur]++) return 0;
for (int Flow, To = 1; To <= n; To++)
{
Рассматриваем ребро (vCur, To).
if
(m[vCur][To] > 0 &&
(Flow =
AugPath(To,Final,min(CurFlow,m[vCur][To]))))
{
m[vCur][To] -= Flow; m[To][vCur] += Flow;
return
Flow;
}
}
return 0;
}
Основная часть
программы. Читаем входные данные. Если граф содержит мультиребра между
вершинами a и b с пропускными способностями с1,
с2, …, ck, то считаем что имеется одно
ребро между a и b с пропускной способностью с1
+ с2 + … + ck.
scanf("%d %d",&n,&Edges);
memset(m,0,sizeof(m));
while (Edges--)
scanf("%d %d
%d",&a,&b,&c), m[a][b] += c, m[b][a] += c;
Пока существует дополняющий путь,
увеличиваем величину потока MaxFlow между истоком 1 и стоком n.
MaxFlow = 0;
do
{
memset(used,0,sizeof(used));
} while ((flow = AugPath (1,n,0x7FFFFFFF)) &&
(MaxFlow += flow));
Выводим максимальный поток.
printf("%d\n",MaxFlow);
Эдмондс – Карп реализация
#include <cstdio>
#include <cstring>
#include <queue>
#define MAX 120
#define INF 2000000000
using namespace
std;
int m[MAX][MAX], used[MAX], parent[MAX];
int a, b, c, flow, MaxFlow, n, Edges;
void bfs(int
v)
{
queue<int>
q;
q.push(v); used[v] = 1;
while(!q.empty())
{
int from =
q.front(); q.pop();
if (from
== n) return;
for(int to = 1; to <= n; to++)
if
((m[from][to] > 0) && (!used[to]))
{
used[to] = 1;
parent[to] = from;
q.push(to);
}
}
}
void Rebuild(int
k, int flow)
{
if (parent[k]
== -1) return;
Rebuild(parent[k],flow);
m[parent[k]][k] -= flow;
m[k][parent[k]] += flow;
}
int FindFlow(int
k)
{
if (parent[k]
== -1) return INF;
int x =
FindFlow(parent[k]);
return
min(x,m[parent[k]][k]);
}
int main(void)
{
scanf("%d
%d",&n,&Edges);
memset(m,0,sizeof(m));
while
(Edges--)
{
scanf("%d
%d %d",&a,&b,&c);
m[a][b] += c; m[b][a] += c; // multiedges
}
MaxFlow = 0;
while(1)
{
memset(parent,-1,sizeof(parent));
memset(used,0,sizeof(used));
bfs(1);
flow
= FindFlow(n);
if (flow ==
INF) break;
MaxFlow += flow;
Rebuild(n,flow);
}
printf("%d\n",MaxFlow);
return 0;
}
Диниц реализация
#include <cstdio>
#include <cstring>
#define MAX 120
#define INF 0x3F3F3F3F
using namespace
std;
int Cap[MAX][MAX], CurFlow[MAX][MAX],
used[MAX], d[MAX],
q[MAX], ptr[MAX];
int a, b, c, MaxFlow, n, Edges;
int min(int
i, int j)
{
return (i
< j) ? i : j;
}
int bfs(int
s)
{
int qh =
q[qt++] = s;
memset (d, -1, sizeof(d));
d[s] = 0;
while (qh
< qt)
{
int v =
q[qh++];
for (int to = 1; to <= n; to++)
if ((d[to]
== -1) && (CurFlow[v][to] < Cap[v][to]))
{
q[qt++] = to;
d[to] = d[v] + 1;
}
}
return d[n]
!= -1;
}
int dfs(int
v, int flow)
{
if
(!flow) return
0;
if (v ==
n) return
flow;
for (int &to = ptr[v]; to <= n; to++)
{
if (d[to]
!= d[v] + 1) continue;
int pushed
= dfs (to, min (flow, Cap[v][to] - CurFlow[v][to]));
if (pushed)
{
CurFlow[v][to] += pushed;
CurFlow[to][v] -= pushed;
return
pushed;
}
}
return 0;
}
int Dinic(int
s)
{
int flow = 0;
for (;;)
{
if
(!bfs(s)) break;
memset(ptr,0,sizeof(ptr));
while (int pushed = dfs (s, INF))
flow += pushed;
}
return flow;
}
int main(void)
{
scanf("%d
%d",&n,&Edges);
memset(Cap,0,sizeof(Cap));
memset(CurFlow,0,sizeof(CurFlow));
while
(Edges--)
scanf("%d
%d %d",&a,&b,&c), Cap[a][b] += c, Cap[b][a] += c;
MaxFlow = Dinic(1);
printf("%d\n",MaxFlow);
return 0;
}